分类问题的模型评价指标

在回归问题中，我们可能会采用均方误差衡量模型的好坏。但在分类问题中，我们需要判断模型是否被正确分类了，于是有如下的评价标准：

True表示预测正确，False表示预测错误，将负例错误预测称为1型错误，将正例错误的预测成负例被称为2型错误。

• 准确率(Accuracy)=预测正确的样本数/总样本数

• 精确率(Precision)=TP/预测为正例的样本数

• 召回率(Recall)=TP/样本真实值为正例的样本数

• F值=Precision和Recall的调和平均值

我们可以理解为：

准确率(Accuracy)就是所有样本中预测正确的比例。

精确率(Precision)从某个预测结果出发，其中预测正确的比例。

召回率(Recall)从某个类别的真实样本出发，其中被正确预测的比例。

F值是精确率和召回率的调和平均数。

总结：

从2类真实值出发，根据是否预测正确衍生出了TPR、FNR、FPR、TNR四类指标，分别是真正率，假负率、假正率、真负率。同时可以看到真正率TPR等价于召回率Recall。

混淆矩阵

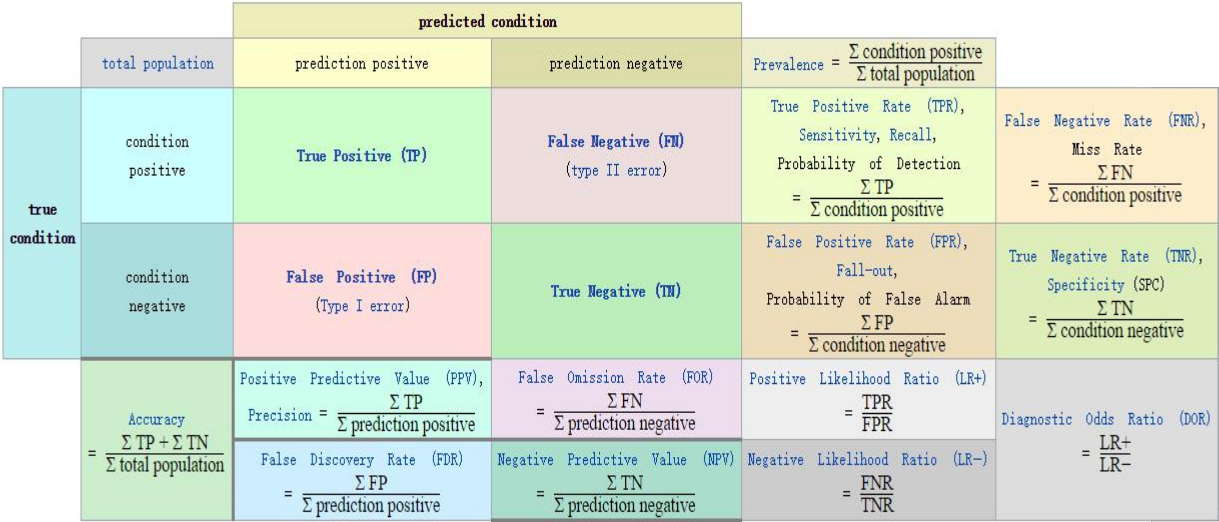
参考：https://en.wikipedia.org/wiki/Precision_and_recall

准确率

$$\text{ Accuracy }=\frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}+\mathrm{T}\mathrm{N}}$$

假如 100 个数据中 80 个被正确地分类了，那么准确率就是0.8。用测试数据来计算这个值，值越高精度越高，也就意味着模型越好。

精确率和召回率

假设图中的圆点是 Positive 数据、叉号是Negative 数据：

假设有 100 个数据，其中 95 个是 Negative。那么，哪怕出现模型把数据全部分类为 Negative 的极端情况，Accuracy 值也为 0.95，也就是说模型的精度是 95%。但是不管精度多高，一个把所有数据都分类为 Negative 的模型，不能说它是好模型。

假设我们的模型分类结果如下：

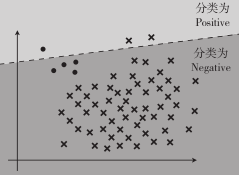
精确率：
$$\text{ Precision }=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}$$
这个指标只关注分类为 Positive 的数据中，实际就是 Positive 的数据所占的比例：

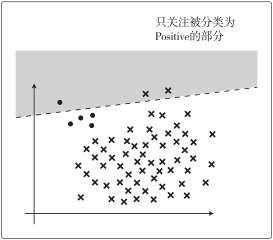
从图中可以看到，精确率=1/3

召回率：
$$\text{ Recall }=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$$
这个指标只关注实际是Positive 的数据中，被正确分类的比例：

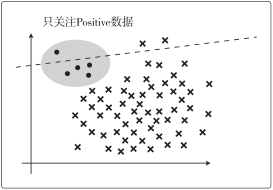
从图中可以看到，召回率=1/5

F 值

上面的例子说明准确率很高的模型，精确率和召回率都可以非常低。
$$\text{ Fmeasure }=\frac{2}{\frac{1}{\text{ Precision }}+\frac{1}{\text{ Recall }}}$$
该指标考虑到了精确率和召回率的平衡，精确率和召回率只要有一个低，就会拉低 F 值。

该公式变形后为：
$$\text{ Freasure }=\frac{2\cdot \text{ Precision }\cdot \text{ Recall }}{\text{ Precision }+\text{ Recall }}$$
称 F 值为 F1 值会更准确，因为除 F1 值之外，还有带权重的 F 值指标：
$$\text{ WeightedFmeasure }=\frac{\left(1+{\beta }^2\right)\cdot \text{ Precision }\cdot \text{ Recall }}{{\beta }^2\cdot \text{ Precision }+\text{ Recall }}$$

ROC与AUC

ROC（Receiver Operating Characteristic） 描述的是FPR-TPR两个量之间的相对变化情况，纵轴是“真正率”（True Positive Rate 简称TPR），横轴是“假正率” （False Positive Rate 简称FPR）。ROC反映了TPR随着FPR递增的情况下，谁增长得更快，快多少的问题。TPR增长得越快，曲线越往上屈，AUC就越大，反映了模型的分类性能就越好。

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。AUC作为ROC曲线的具体数值可以直观的评价分类器的好坏，值越大越好。

• AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

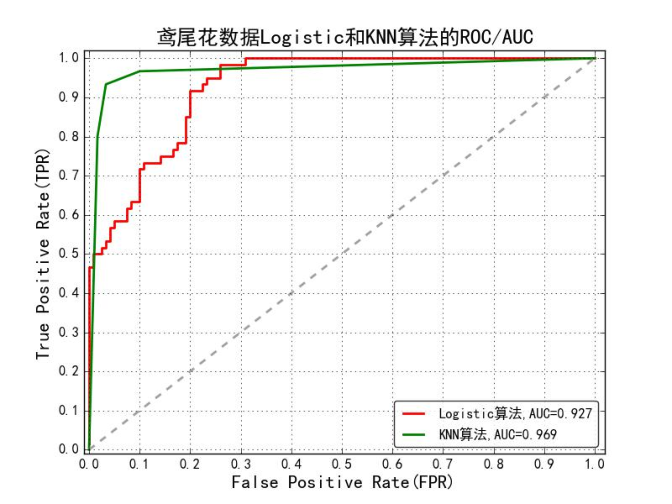
当数据样本不平衡的时候，为什么采用 ROC 做评估指标比较好？

我们知道TPR 只与正样本有关，FPR 只与负样本有关。假设总样本中 10% 是正样本、90% 是负样本，计算 TPR 时只需要考虑 10% 正样本预测的结果，计算 FPR 时只需要 90% 负样本的预测结果。这样无论样本分布是怎么样的，都不影响 TPR 和 FPR 的计算，也就不会影响 ROC 曲线的趋势。

各评价指标对于的sklearn函数

指标	描述	scikit-learn函数
Precision	精确度	from sklearn.metrics import precision_score
Recall	召回率	from sklearn.metrics import recall_score
F1	F1指标	from sklearn.metrics import f1_score
Confusion Matrix	混淆矩阵	from sklearn.metrics import confusion_matrix
ROC	ROC曲线	from sklearn.metrics import roc
AUC	ROC曲线下的面积	from sklearn.metrics import auc