大家好，我是小小明。

今天看到了一道我做不出来的小学数学题：

目前的要求就是要求出阴影部分的面积：

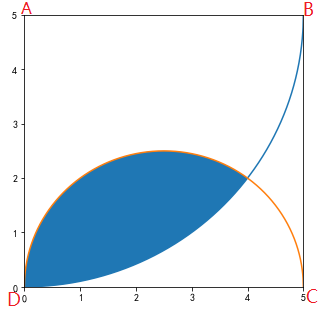
虽说只是一道小学数字题，但作为渣渣我是真的不会做。虽然我不会做，但是我会Python，所以可以让Python帮我做。

不过这题张老师会做，这是他的解法：

张老师的解法

首先作辅助线：

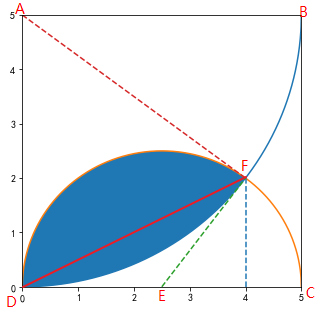
根据容斥原理，S(阴影部分面积)=S(扇形DAF)+S(扇形DEF)-S(四边形AFED)

S(四边形AFED)=2*S(三角形ADE)=1/2*S(正方形ABCD)=25/2

两个扇形的面积求解会复杂点，但只要找到相似三角形就能找到突破点。

因为∠AFE=∠ADE=90°，所以∠DAF+∠FED=180°

又∠FEC+∠FED=180°，所以∠DAF=∠FEC

故 扇形DAF 与 扇形FEC 相似。

对于相似扇形，面积之比等于边长之比的平方。

因为AD=2*EC，所以S(扇形DAF)=4*S(扇形FEC)

所以S(扇形DAF)+S(扇形DEF)=4*S(扇形FEC)+S(扇形DEF)=3*S(扇形FEC)+S(半圆DC)

$S(\text{扇形FEC})=\frac{\angle FEC}{2\pi }\cdot \pi \cdot (\frac{5}{2}{)}^2=\frac{25\cdot \angle FEC}{8}$

由于∠FEC=∠DAF，故$S(\text{扇形FEC})=\frac{25\cdot \angle DAF}{8}$

下面我们求解∠DAF，由于tan(∠DAE)=DE/AD=1/2

根据倍角公式：$\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }$得

$tan(\angle DAF)=tan(2\ast \angle DAE)=\frac{2\cdot \frac{1}{2}}{1-{(\frac{1}{2})}^2}=\frac{1}{\frac{3}{4}}=\frac{4}{3}$

所以，∠DAF=arctan(4/3)

所以S(阴影部分面积)=S(扇形DAF)+S(扇形DEF)-S(四边形AFED)

=3*S(扇形FEC)+S(半圆DC)-25/2

=3·(25·arctan(4/3)/8)+((5/2)^2·π)/2-25/2

=75/8·arctan(4/3)+25/8·π-25/2

这样就得到了最终结果为：=75/8·arctan(4/3)+25/8·π-25/2

用python计算一下精确数值：

import math

75/8*math.atan(4/3)+25/8*math.pi-25/2

结果：6.0108697112332194

在计算出∠DAF后，算阴影部分的弧长也很简单了：

DF的上弧长=DC弧长-FC弧长=5/2·π-5/2·arctan(4/3)

DF的下弧长=5·∠DAF=5·arctan(4/3)

阴影部分的弧长=DF的上弧长+DF的下弧长=5/2·π+5/2·arctan(4/3)

用python计算一下精确数值：

import math

5/2*math.pi+5/2*math.atan(4/3)

结果：10.172219678978513

个人感觉上面的解法虽然计算出来了，还是挺复杂的，直接用python计算积分简单省事：

Python绘制函数图形

首先，我们以D点建立直角坐标系，然后计算出，扇形和圆形的函数分别是：

• 扇形：$y=5-\sqrt{25-x^2}$
• 圆形：$y=\sqrt{5x-x^2}$

绘制图形验证一下：

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
%matplotlib inline

x = np.linspace(0, 5, 1024)
y1 = 5-np.sqrt(25-x**2)
y2 = np.sqrt(5*x-x**2)

plt.figure(figsize=(5, 5))
plt.plot(x, y1, label='扇形y=5-$\sqrt{25-x^2}$')
plt.plot(x, y2, label='圆形y=$\sqrt{5x-x^2}$')
plt.fill_between(x[y1 <= y2], y1[y1 <= y2], y2[y1 <= y2])
plt.xlim(0, 5)
plt.ylim(0, 5)
plt.axvline(4, ymin=0, ymax=0.4, color="r", ls="--")
plt.legend()

plt.show()

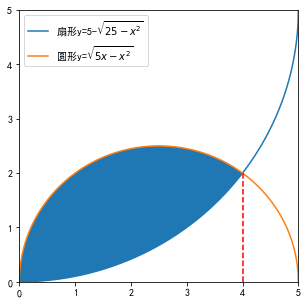
从结果看没有问题。

Python求解积分计算阴影部分面积

上面已经计算出了函数表达式，现在我们使用sympy表示一下：

from sympy.abc import x
import sympy

y1 = 5-sympy.sqrt(25-x**2)
y2 = sympy.sqrt(5*x-x**2)

为了确定积分的结束位置，我们首先需要计算出两个函数的交点。

令两个函数的差值为0，求解x：

sympy.solve(y2-y1, x)

得到：[0, 4]

说明第二个交点的x坐标是4。

为了得到对应的y坐标，我们可以将x代入两个函数任意一个：

display(y1)
display(y1.subs(x, 4))
display(y2)
display(y2.subs(x, 4))

说明交点的y坐标为2。

然后计算积分：

r1 = sympy.integrate(y2-y1, (x, 0, 4))
r1

结果：

$-\frac{25}{2}-\frac{25\mathrm{asin}\left(\frac{\sqrt{5}}{5}\right)}{4}+\frac{25\pi }{8}+\frac{25\mathrm{asin}\left(\frac{4}{5}\right)}{2}$

计算具体的数值：

r1.evalf()

结果为：6.01086971123322

可以看到与张老师的计算结果几乎一致。

Python求解曲线积分计算阴影部分周长

首先，我们需要清楚曲线积分的计算公式：

那么，我们的计算方法为：

r2 = sympy.integrate(sympy.sqrt(1+sympy.diff(y1, x)**2), (x, 0, 4)) + \
    sympy.integrate(sympy.sqrt(1+sympy.diff(y2, x)**2), (x, 0, 4))
r2

结果：

$5\mathrm{asin}\left(\frac{4}{5}\right)+\frac{5\underset{0}{\overset{4}{\int }}\frac{\sqrt{\frac{1}{5-x}}}{\sqrt{x}}dx}{2}$

计算具体的数值：

r2.evalf()

结果为：10.1722196789785