大家好，我是小小明，在学习好友叶庭云介绍的一门中国大学MOOC的课程中，学到手绘图像，下面我测试并总结一下。

课程链接是：https://www.icourse163.org/course/BIT-1001870002?from=searchPage

下面使用Python Imaging Library ( PIL ) 进行图像处理，安装方式：

pip install pillow

彩色图片转手绘线稿的原理简述

对于一张手绘图，其特征主要是边界线条较重、相同或相近色彩趋于白色、略有光源效果。

将彩色图片转换为手绘线稿，首先需要将图片转换为灰度图片。

灰度值实际代表了图像明暗的变化，而梯度代表了灰度的变化率。

调整像素的梯度值可以间接改变图像的明暗程度。

下面以如下图片为例进行测试：

from PIL import Image
import numpy as np

im = Image.open('001.jpg')
im

转换为灰度模式：

im = im.convert("L")
im

png

获取灰度图片像素点数据的numpy数组：

data = np.array(im)
data.shape, data.dtype

((300, 300), dtype('uint8'))

调整像素的梯度值

调整像素的梯度值间接改变图像的明暗程度

首先提取出x和y方向的梯度：

grad_x, grad_y = np.gradient(data)
print(grad_x.shape, grad_y.shape)

(300, 300) (300, 300)

深度值的取值范围为0-100，决定了梯度的缩放比例，现在预设深度值为10：

depth = 10
grad_x /= 100/depth
grad_y /= 100/depth

光源效果

根据灰度变化来模拟人类视觉的远近程度

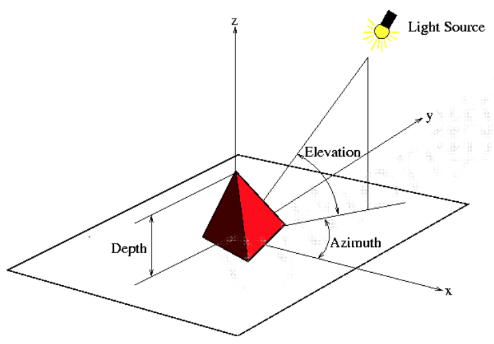
设计一个位于图像斜上方的虚拟光源
光源相对于图像的俯视角为 eLevation，方位角为 Azimuth
建立光源对个点梯度值的影响函数
运算出各点的新像素值

]

假设俯视角eLevation= $\frac \pi {2.2}$ ，方位角Azimuth= $\frac \pi {4}$ ：

eLevation = np.pi / 2.2
azimuth = np.pi / 4
# 光源对x/y/z轴三个方向的影响程度
dx = np.cos(eLevation) * np.cos(azimuth)
dy = np.cos(eLevation) * np.sin(azimuth)
dz = np.sin(eLevation)

梯度归一化

构造x和y轴梯度的三维归一化单位坐标系：

A = np.sqrt(grad_x ** 2 + grad_y ** 2 + 1.)
uni_x = grad_x / A
uni_y = grad_y / A
uni_z = 1. / A

梯度与光源相互作用，将梯度转化为灰度：

b = 255 * (dx * uni_x + dy * uni_y + dz * uni_z)

最终看看转换效果：

Image.fromarray(b.clip(0, 255).astype('uint8'))

代码封装

from PIL import Image
import numpy as np
from PIL.ImageFile import ImageFile
from typing import Union


def img2sketch(img: Union[str, ImageFile], depth=10, eLevation=np.pi / 2.2, azimuth=np.pi / 4):
    assert isinstance(img, str) or isinstance(img, ImageFile)
    assert 0 < depth <= 100
    if isinstance(img, str):
        im = Image.open(img)
    else:
        im = img
    data = np.array(im.convert("L"))
    grad_x, grad_y = np.gradient(data)

    # 根据深度缩放梯度
    grad_x /= 100/depth
    grad_y /= 100/depth

    # 光源对x/y/z轴三个方向的影响程度
    dx = np.cos(eLevation) * np.cos(azimuth)
    dy = np.cos(eLevation) * np.sin(azimuth)
    dz = np.sin(eLevation)

    # 构造x和y轴梯度的三维归一化单位坐标系
    A = np.sqrt(grad_x ** 2 + grad_y ** 2 + 1.)
    uni_x = grad_x / A
    uni_y = grad_y / A
    uni_z = 1. / A

    # 梯度与光源相互作用，将梯度转化为灰度
    b = 255 * (dx * uni_x + dy * uni_y + dz * uni_z)

    return Image.fromarray(b.clip(0, 255).astype('uint8'))

调整一下深度和光源方向测试一下：

img2sketch('001.jpg', 5, azimuth=-5/4*np.pi)

图像处理中的三个基本操作

反相：

对于三通道的RGB图片：

t = [255, 255, 255] - data    # 计算RGB三个通道的补值
Image.fromarray(t.astype('uint8'))

对于单通道的灰度图片：

t = 255 - data
Image.fromarray(t.astype('uint8'))

区间变换（灰度图像）：

t = (100 / 255) * data + 150   # 区间变换
Image.fromarray(t.astype('uint8'))

像素取平方（灰度图像）：

t = 255 * (data / 255) ** 2    # 像素平方
Image.fromarray(e.astype('uint8'))

Biegral Blog