各位小伙伴大家好,今天我将给大家演示一个非常高级的工具,SMT求解器。应用领域非常广,解各类方程,解各类编程问题(例如解数独),解逻辑题等都不在话下。
今天小小明就将带大家看看这其中的精彩:

文章目录
🎨z3-solver求解器🎨
🔦简介🔫
z3-solver是由Microsoft Research(微软)开发的SMT求解器,它用于检查逻辑表达式的可满足性,可以找到一组约束中的其中一个可行解,缺点是无法找出所有的可行解(对于规划求解问题可以是scipy)。
z3-solver可应用于软/硬件的验证与测试、约束求解、混合系统的分析、安全、生物,以及几何求解等问题。Z3 主要由 C++ 开发,提供了 .NET、C、C++、Java、Python 等语言调用接口,下面以python接口展开讲解。
z3可直接通过pip安装:
pip install z3-solver
参考示例:https://ericpony.github.io/z3py-tutorial/guide-examples.htm
z3中有3种类型的变量,分别是整型(Int),实型(Real)和向量(BitVec)。
对于整数类型数据,基本API:
- Int(name, ctx=None),创建一个整数变量,name是名字
- Ints (names, ctx=None),创建多个整数变量,names是空格分隔名字
- IntVal (val, ctx=None),创建一个整数常量,有初始值,没名字。
对于实数类型的API与整数类型一致,向量(BitVec)则稍有区别:
- Bitvec(name,bv,ctx=None),创建一个位向量,name是他的名字,bv表示大小
- BitVecs(name,bv,ctx=None),创建一个有多变量的位向量,name是名字,bv表示大小
- BitVecVal(val,bv,ctx=None),创建一个位向量,有初始值,没名字。
simplify(表达式),对可以简化的表达式进行简化。
完整API文档可参考:https://z3prover.github.io/api/html/namespacez3py.html
下面我们看看z3的基本用法:
🔀数学运算🎦
先以一个简单例子入门:
♊️二元一次方程♋️
比如使用z3解二元一次方程:
x − y = 3 x-y = 3 x−y=3
3 x − 8 y = 4 3x-8y=4 3x−8y=4
solve直接求解:
from z3 import *
x, y = Reals('x y')
solve(x-y == 3, 3*x-8*y == 4)
[y = 1, x = 4]
如果需要取出指定变量的结果,可以使用Solver求解器:
- s=solver(),创建一个解的对象。
- s.add(条件),为解增加一个限制条件
- s.check(),检查解是否存在,如果存在,会返回"sat"
- modul(),输出解得结果
x, y = Reals('x y')
solver = Solver()
qs = [x-y == 3, 3*x-8*y == 4]
for q in qs:
solver.add(q)
if solver.check() == sat:
result = solver.model()
print(result)
print("x =", result[x], ", y =", result[y])
[y = 1, x = 4]
x = 4 , y = 1
可以通过solver.assertions()查看求解器已经添加的约束和约束的个数:
assertions = solver.assertions()
print(assertions)
print(len(assertions))
[x - y == 3, 3*x - 8*y == 4]
2
如果需要删除约束条件,则需要在添加约束前调用solver.push()方法。
下面我们如下方程为例进行演示:
x > 10 x > 10 x>10
y = x + 2 y = x + 2 y=x+2
获取结果:
x, y = Ints('x y')
solver = Solver()
solver.add(x > 10, y == x + 2)
print("当前约束:", solver.assertions())
if solver.check() == sat:
print("结果:", solver.model())
else:
print(solver.check())
当前约束: [x > 10, y == x + 2]
结果: [x = 11, y = 13]
下面我们再增加一个可以被删除的约束y < 11:
solver.push()
solver.add(y < 11)
print("当前约束:", solver.assertions())
if solver.check() == sat:
print("结果:", solver.model())
else:
print(solver.check())
当前约束: [x > 10, y == x + 2, y < 11]
unsat
可以看到这种约束下,无有效解。
删除约束,再计算一次:
solver.pop()
print("当前约束:", solver.assertions())
if solver.check() == sat:
print("结果:", solver.model())
else:
print(solver.check())
当前约束: [x > 10, y == x + 2]
结果: [x = 11, y = 13]
⚠️注意:没有push过的约束条件时直接pop会导致报出
Z3Exception: b'index out of bounds'错误。
🚦线性多项式约束🚧
约束条件为:
x
>
2
y
<
10
x
+
2
∗
y
=
7
x > 2 \\ y < 10 \\ x + 2 * y = 7 \\
x>2y<10x+2∗y=7
上述约束x和y都是整数,我们需要找到其中一个可行解:
x, y = Ints('x y')
solve([x > 2, y < 10, x + 2*y == 7])
结果:
[y = 0, x = 7]
当然,实际可行的解不止这一个,z3只能找到其中一个可行的解。
💧非线性多项式约束🌌
约束条件为:
x 2 + y 2 > 3 x^2 + y^2 > 3 x2+y2>3
x 3 + y < 5 x^3 + y < 5 x3+y<5
上述约束x和y都是实数,我们需要找到其中一个可行解:
x, y = Reals('x y')
solve(x**2 + y**2 > 3, x**3 + y < 5)
结果:
[y = 2, x = 1/8]
很快就计算出了一个可行解。
上面我演示了一些基础的例子,下面继续分享综合一些的案例:
💫高中物理匀变速直线运动相关问题📰
高中物理中的匀变速直线运动公式为:
s = v i t + 1 2 a t 2 s=v_it + \frac12at^2 s=vit+21at2
v f = v i + a t v_f=v_i + at vf=vi+at
举个例子,以30m/s的速度前进时踩下刹车,如果减速的加速度为 − 8 m / s 2 -8m/s^2 −8m/s2,求刹车完毕时,汽车的刹车距离是多少?
直接解题:
s, v_i, a, t, v_f = Reals('s v__i a t v__f')
equations = [
s == v_i*t + (a*t**2)/2,
v_f == v_i + a*t,
]
print("运动方程:", equations)
variables = [
v_i == 30,
v_f == 0,
a == -8
]
print("参数变量:", variables)
print("结果:")
solve(equations + variables)
运动方程: [s == v__i*t + (a*t**2)/2, v__f == v__i + a*t]
参数变量: [v__i == 30, v__f == 0, a == -8]
结果:
[a = -8, v__f = 0, v__i = 30, t = 15/4, s = 225/4]
可以看到刹车距离是225/4m,刹车历时15/4s。
需要获取指定变量的结果则需要Solver求解器:
solver = Solver()
equations = [
s == v_i*t + (a*t**2)/2,
v_f == v_i + a*t,
]
variables = [
v_i == 30,
v_f == 0,
a == -8
]
solver.add(equations + variables)
if solver.check() == sat:
result = solver.model()
print(f"刹车距离:{result[s].as_decimal(4)}m,刹车时间:{result[t].as_decimal(4)}s")
刹车距离:56.25m,刹车时间:3.75s
到这里,大家算是已经对z3的用法入门了。下面我继续演示一些更高级的内容,使用z3解决一些编程上的问题:
📜综合性编程问题📈
📐解数独✏️
之前我演示过程序自动玩数独:
文中对于一个困难级别的数独,python优化后的算法耗时达到3.2秒,核心逻辑使用C语言改写后耗时达到毫秒级。
下面我使用z3求解器来解决这个问题,这样可以在不使用其他语言开发的情况,纯Python就能达到不错的性能。
首先,我们根据数独游戏的规则创建约束条件:
from z3 import *
# 9x9 整数变量矩阵
X = [[Int(f"x_{i}_{j}") for j in range(9)]
for i in range(9)]
# 每个单元格在 1,2,3,...8,9 中包含一个值
cells_c = [And(1 <= X[i][j], X[i][j] <= 9)
for i in range(9) for j in range(9)]
# 每行每个数字最多出现一次
rows_c = [Distinct(X[i]) for i in range(9)]
# 每列每个数字最多出现一次
cols_c = [Distinct([X[i][j] for i in range(9)])
for j in range(9)]
# 每个 3x3 方格每个数字最多出现一次
sq_c = [Distinct([X[3*i0 + i][3*j0 + j]
for i in range(3) for j in range(3)])
for i0 in range(3) for j0 in range(3)]
# 数独完整约束条件
sudoku_c = cells_c + rows_c + cols_c + sq_c
依然针对之前那个Python耗时3秒多的数独:
# 需要求解的数独,0表示空单元格
board = [
[0, 0, 0, 6, 0, 0, 0, 3, 0],
[5, 0, 0, 0, 0, 0, 6, 0, 0],
[0, 9, 0, 0, 0, 5, 0, 0, 0],
[0, 0, 4, 0, 1, 0, 0, 0, 6],
[0, 0, 0, 4, 0, 3, 0, 0, 0],
[8, 0, 0, 0, 9, 0, 5, 0, 0],
[0, 0, 0, 7, 0, 0, 0, 4, 0],
[0, 0, 5, 0, 0, 0, 0, 0, 8],
[0, 3, 0, 0, 0, 8, 0, 0, 0]
]
求解:
def solveSudoku(board: list):
board_c = [If(board[i][j] == 0,
True,
X[i][j] == board[i][j])
for i in range(9) for j in range(9)]
s = Solver()
s.add(sudoku_c + board_c)
if s.check() == sat:
m = s.model()
r = [[m[X[i][j]].as_long() for j in range(9)]
for i in range(9)]
return r
solveSudoku(board)
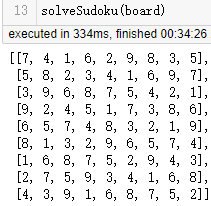
可以看到在0.3秒多的时间内已经计算出结果,而且结果与之前的结果一致:

🍞八皇后问题🍩
有一个 8x8 的棋盘,希望往里放 8 个棋子(皇后),每个棋子所在的行、列、对角线都不能有另一个棋子。
下图中左图是满足条件的一种方法,又图是不满足条件的。八皇后问题就是期望找到满足这种要求的放棋子方式:
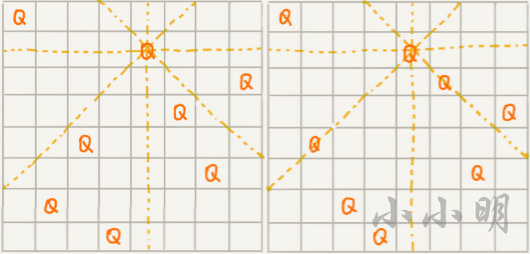
如果我们要求找到所有满足条件的解,则只想使用回溯算法进行递归求解,但是如果只需要一个可行解时,我们则可以使用z3求解器。
首先创建约束条件:
# 每个皇后必须在不同的行中,记录每行对应的皇后对应的列位置
Q = [Int(f'Q_{i}') for i in range(8)]
# 每个皇后在列 0,1,2,...,7
val_c = [And(0 <= Q[i], Q[i] <= 7) for i in range(8)]
# 每列最多一个皇后
col_c = [Distinct(Q)]
# 对角线约束
diag_c = [If(i == j,
True,
And(Q[i] - Q[j] != i - j, Q[i] - Q[j] != j - i))
for i in range(8) for j in range(i)]
直接求解可以得到一个可行解中,其中每个皇后的列位置:
solve(val_c + col_c + diag_c)
结果:
[Q_3 = 5,
Q_1 = 1,
Q_7 = 6,
Q_5 = 2,
Q_4 = 0,
Q_0 = 3,
Q_2 = 7,
Q_6 = 4]
当然我们还可以把结果打印的清晰一点:
def print_eight_queen(result):
for column in result:
for i in range(8):
if i == column:
print(end="Q ")
else:
print(end="* ")
print()
s = Solver()
s.add(val_c + col_c + diag_c)
if s.check() == sat:
result = s.model()
result = [result[Q[i]].as_long() for i in range(8)]
print("每行皇后所在的列位置:", result)
print_eight_queen(result)
结果:
每行皇后所在的列位置: [5, 3, 1, 7, 4, 6, 0, 2]
* * * * * Q * *
* * * Q * * * *
* Q * * * * * *
* * * * * * * Q
* * * * Q * * *
* * * * * * Q *
Q * * * * * * *
* * Q * * * * *
🎡安装依赖问题🌈
安装程序时往往存在依赖和冲突的关系,通过z3可以轻松求解正确的包的安装顺序。
例如:
- 包a依赖于包b、c和z
- 包b依赖于包d
- 包c,依赖于d或e,以及f或g
- 包d与包e冲突
- 包d与包g冲突
假设要安装包a编码如下:
from z3 import *
a, b, c, d, e, f, g, z = Bools('a b c d e f g z')
# 1.包a依赖于包b、c和z
q1 = And([Implies(a, dep) for dep in [b, c, z]])
# 2.包b依赖于包d
q2 = Implies(b, d)
# 3.包c,依赖于d或e,以及f或g
q3 = Implies(c, And([Or(d, e), Or(f, g)]))
# 4.包d与包e冲突
q4 = Or(Not(d), Not(e))
# 5.包d与包g冲突
q5 = Or(Not(d), Not(g))
s = Solver()
# 安装包a
s.add(a, q1, q2, q3, q4, q5)
if s.check() == sat:
m = s.model()
# x() 返回Z3表达式,x.name()返回字符串
r = [x.name() for x in m if is_true(m[x])]
print("安装a:")
print(r)
else:
print("无效的安装配置")
安装a:
['z', 'b', 'd', 'f', 'c', 'a']
为了方便调用我们可以将依赖和冲突封装成单独的方法:
def DependsOn(pack, deps):
if is_expr(deps):
return Implies(pack, deps)
else:
return And([Implies(pack, dep) for dep in deps])
def Conflict(*packs):
return Or([Not(pack) for pack in packs])
def install_check(*problem):
s = Solver()
s.add(problem)
if s.check() == sat:
m = s.model()
# x() 返回Z3表达式,x.name()返回字符串
r = [x.name() for x in m if is_true(m[x])]
print(r)
else:
print("无效的安装配置")
再次调用安装a:
a, b, c, d, e, f, g, z = Bools('a b c d e f g z')
print("安装a:")
install_check(
a,
DependsOn(a, [b, c, z]),
DependsOn(b, d),
DependsOn(c, [Or(d, e), Or(f, g)]),
Conflict(d, e),
Conflict(d, g),
)
安装a:
['z', 'b', 'd', 'f', 'c', 'a']
安装a和g:
print("安装a和g:")
install_check(
a,
g,
DependsOn(a, [b, c, z]),
DependsOn(b, d),
DependsOn(c, [Or(d, e), Or(f, g)]),
Conflict(d, e),
Conflict(d, g),
)
安装a和g:
无效的安装配置
可以看到z3成功计算出存在冲突的a和g。
🎢 逻辑题🚊
在解决了编程问题后,我们最后玩两道逻辑题:
🚫谁是盗贼🗿
一军用仓库被窃,公安部门已掌握如下线索:①甲、乙、丙三人至少有一个是窃贼;②如甲是窃贼,则乙一定是同案犯;③盗窃发生时,乙正在影剧院看电影。由此可以推出( )。
A. 甲、乙、丙都是窃贼
B. 甲和乙都是窃贼
C. 丙是窃贼
D. 甲是窃贼
完整解题代码:
# abc分别代表甲、乙、丙是否是盗贼
a, b, c = Bools('a b c')
# 三人至少有一个是窃贼
q1 = Or(a, b, c)
# 如甲是窃贼,则乙一定是同案犯;
q2 = Implies(a, b)
# 乙一定不是
q3 = Not(b)
s = Solver()
s.add(q1, q2, q3)
options = [
# 甲、乙、丙都是窃贼
And(a, b, c),
# 甲甲和乙都是窃贼
And(a, b),
# 丙是窃贼
c,
# 甲是窃贼
a
]
result = []
for answer, option in zip("ABCD", options):
s.push()
s.add(option)
print(answer, s.check(), s.assertions())
if s.check() == sat:
result.append(answer)
s.pop()
print("最终答案:", "".join(result))
A unsat [Or(a, b, c), Implies(a, b), Not(b), And(a, b, c)]
B unsat [Or(a, b, c), Implies(a, b), Not(b), And(a, b)]
C sat [Or(a, b, c), Implies(a, b), Not(b), c]
D unsat [Or(a, b, c), Implies(a, b), Not(b), a]
最终答案: C
上述结果可以看到只有第3条的结果为sat(有解),说明对应的选项 C 是正确的。
⛔️煤矿事故✴️
题目如下:
某大型煤矿发生了一起重大事故,事发现场的人有以下的断定:
矿工甲:发生事故的原因是设备问题;
矿工乙:有人违反了操作规程,但发生事故的原因不是设备问题;
矿工丙:如果发生事故的原因是设备问题,那么有人违反操作规程;
矿工丁:发生事故的原因是设备问题,但没有人违反操作规程。如果上述四人的断定中只有一个人为真,则以下可能为真的一项是( )。
A.矿工甲的断定为真
B.矿工乙的断定为真
C.矿工丁的断定为真
D.矿工丙的断定为真,有人违反了操作规程
E.矿工丙的断定为真,没有人违反操作规程
首先需要定义题目中的两个命题,设备是否有问题和是否有人违反操作规程。
完整解题代码:
equipment = Bool('equipment') # 设备是否有问题
violation = Bool('violation') # 是否违反操作规程
qs = [
# 甲:发生事故的原因是设备问题;
equipment,
# 乙:有人违反了操作规程,但发生事故的原因不是设备问题;
And(violation, Not(equipment)),
# 丙:如果发生事故的原因是设备问题,那么有人违反操作规程;
Implies(equipment, violation),
# 丁:发生事故的原因是设备问题,但没有人违反操作
And(equipment, Not(violation)),
]
s = Solver()
# 上述四人的断定中只有一个人为真
s.add(Sum([If(q, 1, 0) for q in qs]) == 1)
# 逐个判断各个选项是否正确
options = [qs[0], qs[1], qs[3], And(
qs[2], violation), And(qs[2], Not(violation))]
result = []
for answer, option in zip("ABCDE", options):
s.push()
s.add(option)
print(answer, s.check(), s.assertions())
if s.check() == sat:
result.append(answer)
s.pop()
print("最终答案:", "".join(result))
结果:
A unsat [If(equipment, 1, 0) +
If(And(violation, Not(equipment)), 1, 0) +
If(Implies(equipment, violation), 1, 0) +
If(And(equipment, Not(violation)), 1, 0) ==
1,
equipment]
B unsat [If(equipment, 1, 0) +
If(And(violation, Not(equipment)), 1, 0) +
If(Implies(equipment, violation), 1, 0) +
If(And(equipment, Not(violation)), 1, 0) ==
1,
And(violation, Not(equipment))]
C unsat [If(equipment, 1, 0) +
If(And(violation, Not(equipment)), 1, 0) +
If(Implies(equipment, violation), 1, 0) +
If(And(equipment, Not(violation)), 1, 0) ==
1,
And(equipment, Not(violation))]
D unsat [If(equipment, 1, 0) +
If(And(violation, Not(equipment)), 1, 0) +
If(Implies(equipment, violation), 1, 0) +
If(And(equipment, Not(violation)), 1, 0) ==
1,
And(Implies(equipment, violation), violation)]
E sat [If(equipment, 1, 0) +
If(And(violation, Not(equipment)), 1, 0) +
If(Implies(equipment, violation), 1, 0) +
If(And(equipment, Not(violation)), 1, 0) ==
1,
And(Implies(equipment, violation), Not(violation))]
最终答案: E
这些就是z3求解器那些常见的应用,你学费了吗?还想学习python解决规划求解问题,记得关注我等待下一期噢~
我是小小明,咱们下期再见~
